【59歳おじさんのプログラミング挑戦】プラズマ粒子シミュレーションの定式化
こんにちは こんばんは フューチャー・ストラテジスト 高峰 です。
「スーパーコンピューターで色々なことをシミュレーションしているけど、どうやっているのだろう?」
と数値計算(シミュレーション)にご興味がある方に、シミュレーションの方法について解説いたします。
【59歳おじさんのプログラミング挑戦】プラズマ粒子シミュレーションの定式化

コンピューターによるシミュレーションの方法について、今回は、計算できるようにするための手順を、プラズマ粒子シミュレーションの定式化を通じて解説いたいます。
プラズマ現象は宇宙やエネルギー開発だけでなく、身近にもたくさんあります。
- 太陽の中での現象
- 発電のための核融合反応
- 半導体デバイスを製造するプロセス
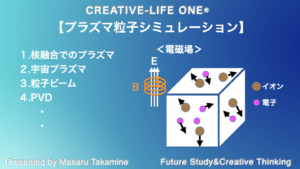
いろいろな場面でプラズマ現象が見られることから、1970年代から、数値シミュレーションは物理モデルの研究開発が取り組まれてきました。
核融合反応の解析がよく知られています。
核融合による発電についての研究は、プラズマと電磁場で閉じ込めて核融合反応を起こす方法と、重水素などの球状物質にレーザーやイオンビームを照射して、爆縮現象により核融合を起こす方法に大別されます。
もっとシンプルに考え、電磁場(E、B)が加わっている立方体内にイオンと電子が分布し、電磁場とイオン、電子が相互作用して運動している現象を数値シミュレーションで解くことを目指します。
この記事では、粒子モデルを用いた、物理モデルとコンピューターで解くための式の導出について簡単にご紹介いたします。
この図に今回対象としている式を記載いたしました。
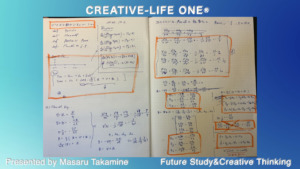
- イオンの運動方程式
- 電子の運動方程式
- 電磁場の式
イオンの運動方程式
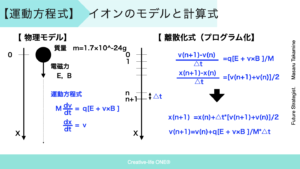
上図のようにイオンの運動方程式は記載されます。
この式では一回の時間微分の式が2個あります。
それぞれを、時間に対して中心差分により離散化します。
その結果、コンピュータで計算できる式に変換することができます。
計算精度や離散化の理論については興味ある方はググってみてください。
電子の運動方程式

上図のように電子の運動方程式は記載されます。イオンとの違いは、電子は非常に軽いため、電磁場で加速されるとすぐに光の速度に達する点です。相対論的効果から、電子は加速されると見かけの重量が増大し、光の速度に漸近(サチュレート)することになります。
この式では一回の時間微分の式が2個あります。
それぞれを、時間に対して中心差分により離散化します。
ここまでは、イオンと同じです。次に、相対論的効果を考慮するために【 M 】の微分式も離散化しておきます。
その結果、コンピュータで計算できる式に変換することができます。
電磁場の式

電磁場の方程式は、イオン電子に比べて少し複雑になります。基本きはマクセル方程式で電場Eと磁場Bがベクトル表記されます。
しかも、マクセル方程式は各要素が絡み合って解きづらくなっています。そこで、ポテンシャルという表記に変化します。
ポテンシャル表記では、ΦとA(ベクトル)のX ,Y,Z成分を分離することができます。
その結果、2回の微分を中心差分を用いて離散化することで、解きやすくなります。
場の方程式を解くには、各座標(格子点)での離散化式の連立方程式を解くことになりますが、これはコンピュータが得意なところです。
【59歳おじさんのプログラミング挑戦】プラズマ粒子シミュレーションの定式化

コンピューターによるシミュレーションの方法について、今回は、計算できるようにするための手順を、プラズマ粒子シミュレーションの定式化を通じて解説いたしました。
興味がある方は、動画もご覧ください。
→プラズマ粒子シミュレーションの定式化
ニュースレターに登録ください。無料で電子書籍を受け取れます。
ニュースレターでは、未来研究と創造思考について情報をお届けいたします。
無料で「自ら、学び、考え、行動するための基本的生活スタイルを学べる電子書籍を受け取りください。









最近のコメント